Coronavirus has become one of the most frequently used words in 2020 and is still causing an impact in people’s life when moving towards 2021. It is undeniably the consequence of the spreading of the coronavirus is tremendous, from the aspect of innumerable deaths to the ineluctable collapse of global economics and international cooperations.
Therefore, the most urgent affair is to control the spread of the virus and prevent a second epidemic, although this is what scientists and professions have been doing for the past year — working on vaccines and using existed statistics to calculate R number, before everything, we need to have a complete mathematical model for COVID-19. Mathematical models are useful to understand the behavior of an infection when it enters a community, and it can used to predict the trend of the virus and the effectiveness of vaccines by using differential equations and computational analysis and therefore producing efficient strategies to minimise the impact of COVID-19. This article will introduce a brief history of the mathematical models used for the epidemic and the role of them in the Coronavirus case.
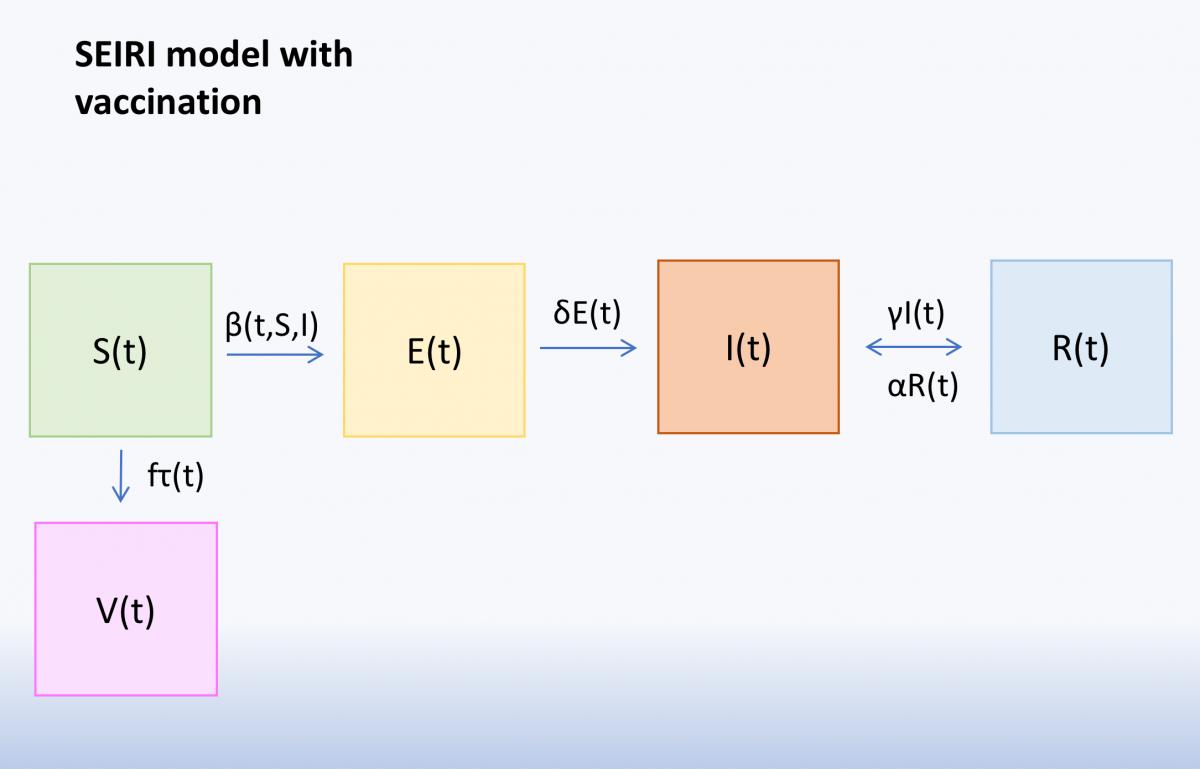
In 1927, W. O. Kermack and A. G. McKendrick created a set of ODEs (ordinary differential equations) — SIR (susceptible, infected, and recovered) epidemic model which is considered under a fixed population, using three compartments to predict statistics. Most of the mathematical models for COVID-19 are based on the SIR model where scientists modified the model catering to characteristics of coronavirus. For example, the SEIR model (shown in figure 1) considered the incubation period and the SIRD model specifies between the recovered (immune) and the deceased (death).
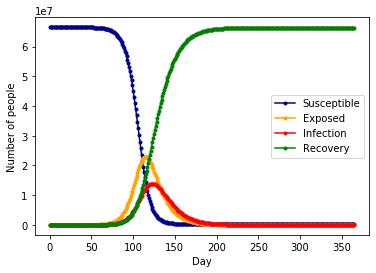
The two significant pieces of information we can derive from figure 1 are: to optimise the situation of the epidemic, we should either attempt to reduce the crest of the infectious graph, therefore, reducing the number of the maximum infectious, or to delay as much as possible the time which the crest occurs. The reason for the second point is, if the peak occurs at the very start of the epidemic, the government is not prepared, the rapid and vast amount of infectious would consume a large number of medical resources and therefore when demand exceeds supply, the deterioration of the virus would cause an increase in the number of infected and the death rate. So we need to delay the peak to enable professions to take steps, for example, to find the sources of the virus and therefore produce effective vaccines.
We might already be familiar with the 'R number', but what it actually means is that the number of people an infectious can spread to. Mathematically, the R number is equal to the transmission rate β divided by the recovery rate γ. R number is essential for public strategies: We need the find valid ways to reduce the transmission rate β and to increase the recovery rate γ. Current provisions such as the enforcement of wearing masks largely decreased the number of infectious as wearing a mask reduces the possibility of potential infectious in a dense population. However, although most countries have the policy of wearing a mask, it is not effective if the mask is not N95 or other respirator masks. Therefore, in other to reduce the transmission rate to the minimum, promoting citizens to wear proper respirator masks is essential.
The second way to reduce the transmission rate is through effective self-isolation/quarantine periods for the exposed population. The quarantine can diagnose potential infectious or asymptomatic individuals. The UK has have been doing effectively in isolating international travelers, but if the virus gets severe again, stricter regulations like isolation for people commuting from different cities in the UK need to be considered.
To retard the time which an epidemic peak will occur (although it is suggested the peak has already occurred in 2020, it is very likely that under the loosening of the policies and the appearance of various mutations, a second or third epidemic will occur in the future), we need to control or reduce the population in specific regions at a given time, that is, lockdown. From my perspective, regional lockdowns for severely infected areas is more practical and effective than a national lockdown. A whole national lockdown still cannot avoid personnel circulation in a single city and a long-term national lockdown would result in an increase in financial deficit and dissatisfaction from citizens. The implementation of smaller lockdowns or semi-lockdowns could help in shortening the time for the epidemic peak.
Last but not least, maximising the recovery rate γ is also an indispensable factor in controlling the epidemic. In 2020, there were many shortages of medical resources such as hospital beds and protective suits for doctors. Currently, the global number of infections has decreased compared to last year, however, we should always be prepared for a potential epidemic in the future. The urgent affair for professions and researchers is to identify the characteristics of the various mutations that appeared and their origins, also to increase the efficiency of the vaccinations. The government, on the other hand, should vaccinate as many people as they could and strengthen international cooperations in vaccination and medical resources to remedy the lack of international business due to COVID-19.
Overall, we can see from a simple mathematical model, we can derive many useful prevention strategies for the epidemic as the model allows us to see a full picture of the virus from the beginning to the future. There is still many development of the epidemic mathematical dynamics model that professions are working on in order to give out more precise predictions by taking into account new variations and other factors.